Curved-crease origami differs from prismatic, or straight-crease origami, in that the folded surface of the pattern is bent during the folding process. They are developable, but with regions of non-zero principal curvature, a combination of attributes have seen them adopted for numerous novel engineering applications. They are also extremely beautiful and so are widely used in fine art, industrial design,and architecture.

Rigid-Foldable Curved-Crease Approximations

To reduce the difficulty in parameterising and modelling the pattern geometry, the curved-crease surface can be approximated as a planar quadrangle (PQ) mesh. Miura-type patterns can be used as a ‘base’ geometry from which to build such curved-crease approximations. The generated curved-crease pattern corresponds to piecewise assembly of self-similar straight-crease patterns and so can be used to simulate a rigid single-DOF folding motion. Further information: DOI: 10.1115/1.4028532.

Elastica Curved-Crease Origami

The analytical geometric construction method was developed for curved-crease origami, that combines a 1D elastica solution for large elastic bending deformation with a straight-crease origami projection and reflection process. This avoids the need for surface discretisation and can thus concisely and accurately capture the principal surface curvature and developability characteristics of elastically-bent curved-crease origami. Further information: DOI: 10.1016/j.ijsolstr.2017.11.029.

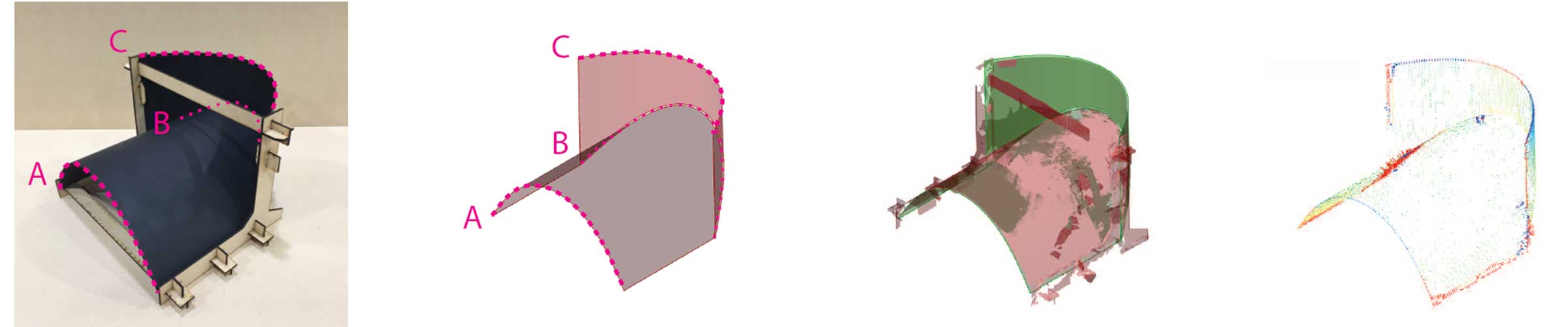
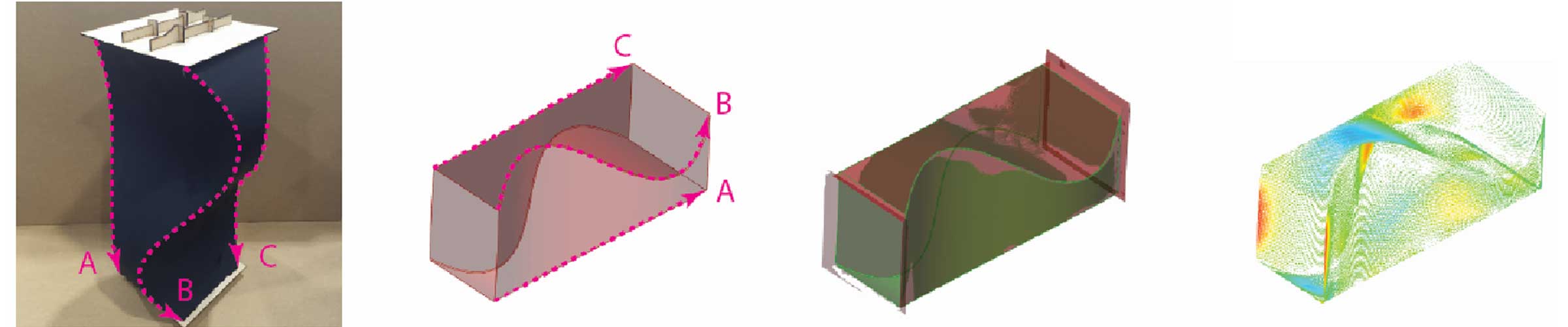
Composite Fabrication Techniques for Curved-Crease Folding

Novel folded fabrication processes have been developed for fibre-reinforced polymer (FRP) composite and FRP-timber hybrid materials. The cured-in-place manufacturing process utilises a differential curing time between two types of resins impregnated in a glass-fibre sheet. A 24-hour slow-cure resin is used on crease lines and a 3-hour fast-cure resin is used on panel regions. The 2D sheet is folded into a 3D section between the fast-cure and slow-cure periods, when panel regions are rigid while hinge regions remain flexible. Further information: Paper 1, Paper 2.

Compliant Curved-Crease Metamaterials

This study introduces a new compliant curved-crease origami-inspired metamaterial with ‘elastica’ non-zero principal surface curvature, differing from traditional straight-crease origami metamaterials. It demonstrates how construction parameters affect non-linear force–displacement responses, including shape, duration, and magnitude. The paper also presents a concise analytical curved-crease bending translation (CCBT) method for quick response prediction and enables the design of metamaterials with programmable compliant force–displacement responses. Further Information: DOI: 10.1016/j.matdes.2021.109859

Related Publications

Lee, T. U., Lu, H., Ma, J., Ha, N. S., Gattas, J. M., & Xie, Y. M. (2024). Self-locking and stiffening deployable tubular structures. Proceedings of the National Academy of Sciences, 121(40), e2409062121. https://doi.org/10.1073/pnas.2409062121

Lee, T.-U., Chen, Y., Heitzmann, M. T., & Gattas, J. M. (2021). Compliant curved-crease origami-inspired metamaterials with a programmable force-displacement response. Materials & Design, 109859. https://doi.org/10.1016/j.ijmecsci.2023.108729

Bukauskas, A., Koronaki, A., Lee, T.-U., Ott, D., Al Asali, M. W., Jalia, A., et al.others. (2021). Curved-crease origami face shields for infection control. Plos one, 16(2), e0245737. https://doi.org/10.1371/journal.pone.0245737

Lee, T.-U., You, Z., & Gattas, J. M. (2018). Elastica surface generation of curved-crease origami. International Journal of Solids and Structures, 136-137, 13–27. https://doi.org/10.1016/j.ijsolstr.2017.11.029

Lee, T., & Gattas, J. (2016). Folded fabrication of composite curved-crease components. In 8th international conference on fibre-reinforced polymer (FRP) composites in civil engineering (CICE 2016). Retrieved from https://espace.library.uq.edu.au/view/UQ:500008

Hansen, B., Tan, J., Gattas, J. M., Fernando, D., & Heitzmann, M. (2016). Folded fabrication of FRP-timber thin-walled beams with novel non-uniform cross-sections. In World conference on timber engineering. Vienna University of Technology. Retrieved from https://espace.library.uq.edu.au/view/UQ:499767

Gattas, J. M., & You, Z. (2014). Miura-base rigid origami: Parametrizations of curved-crease geometries. Journal of Mechanical Design, 136(12), 121404. https://doi.org/https://doi.org/10.1115/1.4028532